LeetCode172 - 阶乘后的零 Py3&C++
本文最后更新于:2021年5月12日 凌晨
793. 阶乘函数后 K 个零
题述
f(x) 是 x! 末尾是 0 的数量。(回想一下 x! = 1 * 2 * 3 * … * x,且 0! = 1 )
例如, f(3) = 0 ,因为 3! = 6 的末尾没有 0 ;而 f(11) = 2 ,因为 11!= 39916800 末端有 2 个 0 。给定 K,找出多少个非负整数 x ,能满足 f(x) = K 。
示例 1:
输入:K = 0
输出:5
解释:0!, 1!, 2!, 3!, and 4! 均符合 K = 0 的条件。
示例 2:
输入:K = 5
输出:0
解释:没有匹配到这样的 x!,符合 K = 5 的条件。
提示:
K 是范围在 [0, 10^9] 的整数。
思路
首先,明确输入输出
题目意思即:output个num!后面有K(即input)个零
疑问句式:阶乘后面有K个零的数有几个?
这题需要了解阶乘尾随零个数的递推公式,根据之前做过的题知道,阶乘尾随零个数已经可以轻松拿到了,那么可以多判几次来数有几个匹配的数,利用这个方法可以先打表看看有啥规律。
先随便设置个最大迭代2000次,从5开始,将结果存进字典里,暴力输出所有解
max_k = 1000
dic = {0: 5}
nums_cnt = 0
for i in range(5, 2*max_k):
nums_cnt += 1
if (trailingZeroes(i) != trailingZeroes(i + 1)):
dic[trailingZeroes(i)] = nums_cnt
nums_cnt = 0
print(f"{trailingZeroes(i)}:{dic[trailingZeroes(i)]}")1:5
2:5
3:5
4:56:5
7:5
8:5
9:5
10:512:5
13:5490:5
492:5
493:5
494:5
495:5
496:5
神奇的发现!输出要么是5要么没有(非5即0)
再看看那些0都是什么输入
# 接上面
zeroes = []
for k in range(0, max_k):
if k not in dic.keys():
zeroes.append(k)
print(zeroes)
5, 11, 17, 23, 29, 30,
36, 42, 48, 54, 60, 61,
67, 73, 79, 85, 91, 92,
98, 104, 110,…
咦好像里面有好多素数,等等!似乎发现了什么不得了的东西!
换个方式打印试试
zeroes = []
for k in range(0, 2000):
if k not in dic.keys():
zeroes.append(k)
# 上面print(zeroes)替换成这个
print("-1", end=',')
for z in range(len(zeroes)-1):
if 6 == (zeroes[z+1] - zeroes[z]):
print(zeroes[z], end=',')
else:
print(zeroes[z], end="\n")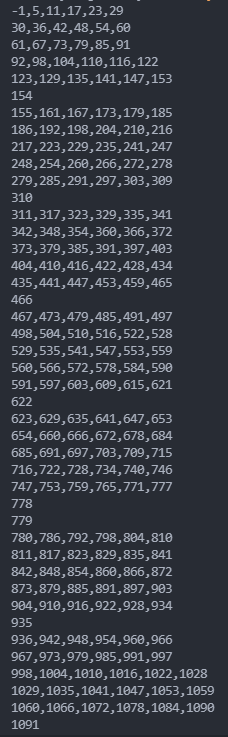
根据打印结果可以发现一些规律了。
或许可以根据这个规律计算出所有没有尾随零的阶乘数,然后打表hhh
数学找规律方法
def preimageSizeFZF(K: int) -> int:
start = 1
while(start < K):
start = start*5+1
while(start > 1):
if (start-1 == K):
return 0
start = (start-1)//5
K %= start
return 5
同样的写法,用C++实现,代码如下:
int preimageSizeFZF(int K) {
int start =1;
while(start < K){
start = start * 5 + 1;
}
while (start>1)
{
if(start==K+1) return 0;
start = (start - 1) / 5;
K %= start;
}
return 5;
}
二分查找法
根据上面找到的规律可以确定答案的范围,于是我们也可以用二分查找的办法来找可行解。
首先,要想尾数有K个,那么那些数肯定大于K,根据前面找出的规律可以发现那些数会小于5*K+1,在此范围内用二分查找,结合之前算阶乘尾随零的算法可以得到代码如下:
int trailingZeroes(long long n) {
return n < 5 ? 0 : (n / 5 + trailingZeroes(n / 5));
}
int preimageSizeFZF(int K) {
switch(K){
case 0:
case 3:
// 打表
return 5;
}
if(K==5) return 0;
long long left = (long long)K;
long long right = 5 * (long long)K + 1;
while(left<right){
long long mid = left + (right - left) / 2;
int tz = trailingZeroes(mid);
if(tz == K) return 5;
if(tz < K) {left = mid + 1;}
else {right = mid;}
}
return 0;
}
这个很快啊!需要注意的就是数据类型要用long long,因为输入可能会超过int范围。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!