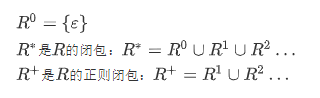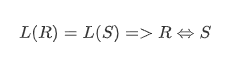编译原理2-词法分析
本文最后更新于:2021年4月9日 下午
# 编译原理2-词法分析
2.0 状态转换图与正规表达式
状态转换图:有限的有向图。圆圈(结点)表示状态,其间用有向边连接,边上可标记字符,表示某一状态接受有向边上的字符/字符集输入后到达另一状态。必有一初态及若干终态,终态结点用双圈表示。终态上用 “ * ”标识表明识别符号时多读了一个其它字符要予以回退,即去掉到终态的有向边上的字符。
[图以后补]
将状态转换图的概念通过正规式加以形式化。
正规表达式(正规式):形式化的表示法,可以表示单词符号的结构,从而精确地定义单词符号集。其表示的集合即正规集。
闭包
如果正规集相等则正规式等价。
(α+ β)*= (α* + β*)*= (α* β*)*
给出语言推正规表达式:最小连接递增倍数闭包
2.1 状态转换图的实现(词法分析器示例)
简单的词法分析器示例,书p13图2-5:
重要函数解释:
token:用来存单词符号的字符串。
concatenation():将token中的字符串与扫描到的字符连接得到新的token。
getbe():过滤空格读字符。
letter() 和 digit():分别用于判断字符类型是否为字母和是否为数字。
retract():扫描指针回退一个字符,并把字符变量置空。
reserve():查是否为保留字,不是则为标识符,返回0。
buildlist():将标识符登记到符号表中或将常数登记到常数表中。
error():出现非法字符报错。
关键部分代码:
token=''; //初始化token数组
s=getchar(); //读字符
getbe(); //过滤空格
switch(s)
{
//遇到字母时
case'a':
...
case'z':
while(letter()||digit()) //当读到字母或数字时
{
concatenation(); //连接组成新token
getchar(); //继续读下一个字符
}
//读到非字母或数字之后跳出循环
retract(); //扫描指针回退一个字符。由于while时多读了一个字符,要退回去再判断
c=reserve(); //读一个字符c,判断c是不是保留字
if(c==0) //如果是标识符(不是保留字)
{
buildlist(); //将标识符登记到符号表里
return(id,指向id的符号表入口指针);
}
else
{
retrn(保留字码,null);
}
break; //到达终态
//遇到数字时
case'0':
...
case'9':
while(digit())
{
concatenation();
getchar();
}
retract();
buildlist();
return(num,num的常数表入口指针);
break;
case'...':
return(...,...);
break;
default:
error(); //剩下的都是非法字符,读到就报错
}2.2 有限自动机FA
有限自动机是更一般化的状态转换图,分为两种:确定有限自动机DFA和非确定有限自动机NFA。
2.2.1 DFA&NFA的表示及区别
有限自动机的表示:五元组(有限状态集,有穷输入字母表,所有的映射函数,初态或初态集,终态集)
区别2即:从同一个状态出发同一字符的出边有多个状态的就是NFA,一个的就是DFA。
DFA输入字符中没有空串ε,NFA中有。
DFA的集合为 ( ),NFA的集合为 { }。
2.2.2 状态转换图和状态转换矩阵
FA M 和 FA M’的等价条件,L(M)=L(M’),即能识别的字符串集相同。
对于任一给定的NFA M,一定存在一个DFA M’ 使得L(M)=L(M’),因此,DFA是NFA的特例。
由正规表达式构造FA
(1)R 等价构造 NFA(R=>NFA)
把R表达式一个一个按优先级拆开,逐个按规则画成拓广转换图。
[书上p21例2.6图2-12以后放]
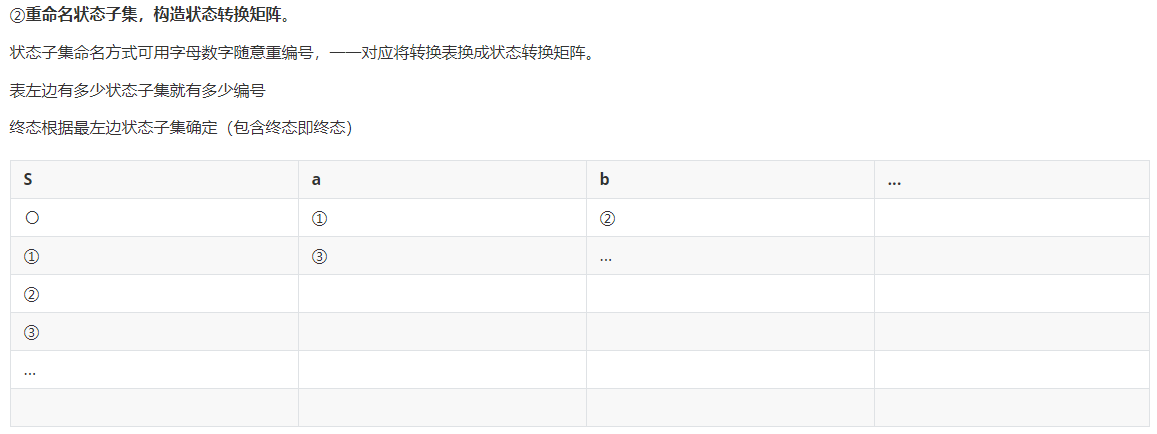
(2)用子集法对NFA 确定化(NFA=> DFA)
用子集法对给定的NFA构造等价的DFA步骤:
根据状态转换表可以得到还没化简的DFA
化简DFA
找一个比 DFA M 状态数少的 DFA M’ 使得 L(M)=L(M’),DFA M’ 满足 1)无多余状态; 2)状态集不存在两个相互等价的状态(即不存在从两个状态出发都能识别同一输入字符串而停于终态)
子集划分法,消除多余状态,合并等价状态。
步骤如下:
先划分终态组和非终态组,再分别考察直至子集不可划分。(可以看转换矩阵的右边是否一样,一样的分一块)
等价可以一块走就凑一块,不等价走不到一块就分开。
把分好组的都排一块编个号
各种表示互相转换
FA五元组<->状态转换图<->状态转换矩阵
典型例题p24 视频词法分析4》21:30
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!