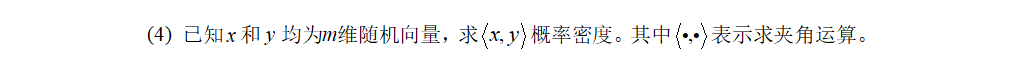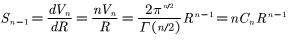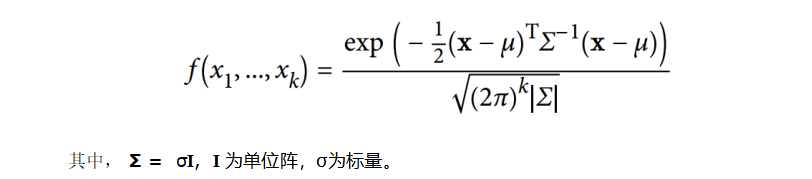# AI算法课数学题4思路–求解m维随机向量两夹角概率密度分布

求解：m维随机向量两夹角概率密度分布

思路

一开始毫无思路，根据问题转化和关键词提取查阅资料后，发现两篇博客n维空间下两个随机向量的夹角分布、空间中两随机向量间夹角的概率密度分布才知道这里可以用n维球体表面积来算，两篇解法异曲同工，最后都是转化到面积微元求积分与整体全积分比值上，涉及n维球体，即超球体，超球面上的随机向量的分布貌似就是球形高斯分布，具有各向同性，

n-1维球体的表面积公式为：

超球面部分参考自百度百科超球面

前面公式里面出现的Gamma函数这里贴一下方便理解：

各向同性的高斯分布（球形高斯分布）指的是各个方向方差都一样的多维高斯分布，协方差为正实数与identity matrix相乘。

因为高斯的circular symmetry，只需要让每个轴上的长度一样就能得到各向同性，也就是说分布密度值仅跟点到均值距离相关，而不和方向有关。

各向同性的高斯每个维度之间也是互相独立的，因此密度方程可以写成几个1维度高斯乘积形式。要注意的是，几个高斯分布乘在一起得到各向同性，但几个Laplace分布相乘就得不到各向同性。

此类高斯分布的参数个数随维度成线性增加，只有均值在增加，而方差是一个标量，因此对计算和存储量的要求不大，因此非常讨人喜欢。

高斯分布部分参考自高斯分布、多维高斯分布、各向同性的高斯分布及多元高斯分布之间的KL散度、读了本文，你就懂了概率分布

求解

在m维超球坐标空间下各个随机向量的分布相当于高斯分布，满足各向同性，等价于单位球面上的均匀分布，只需要考虑单位向量，同时只需要固定其中一个变量，考虑另一个向量的随机变化。（固定向量相对于另一个随机向量也相当于在随机变化）