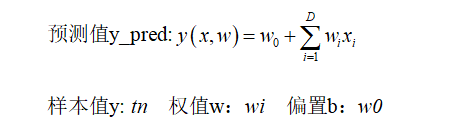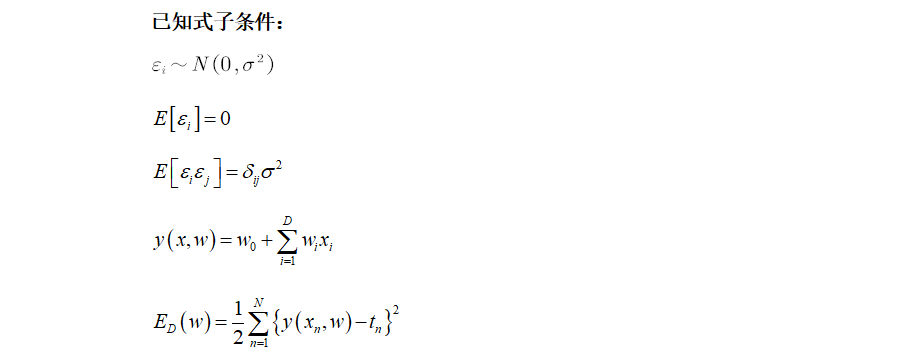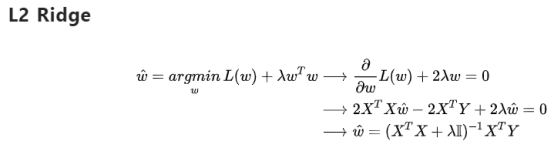# AI算法课数学题2思路–高斯噪声下MLE等价于正则化最小二乘估计

注意！由于没标准答案，不确定是否完全正确，这里仅提供我个人的思路和解法。

证明：高斯噪声下MLE等价于正则化最小二乘估计

思路

参考白板笔记、线性基函数模型

这个应该是b站白板推导里线性回归那几节讲的，平均和误差函数就是损失函数，1/2方便求导，高斯分布的噪声其实就是L2范数，损失函数其实也就是最小二乘法。

相当于最小二乘法（使得平方差之和最小）里的

MLE把先验概率分布看作是均匀分布，先验概率是常数，所以就像是MAP的一个特例

正则化里是利用加法，而MAP里是利用乘法。

证明

根据题意，“对附加权值衰减的正则化项的⽆噪声输⼊变量的平⽅和误差函数进⾏最⼩化，其中偏置参数$w_0$从正则化项中被省略掉。”即L2正则化最小二乘估计；“对在噪声分布上做平均的$E_D$进⾏最⼩化”即噪声为高斯分布的MLE(极大似然估计)。

原题证明转化为：

要不是《统计学习方法》书上课后题好像有类似的，不然题都读不明白，完全没思路orz

。