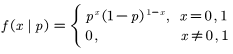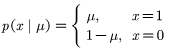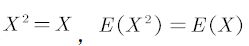# AI算法课数学题1思路–伯努利分布性质证明

注意！由于没标准答案，不确定是否完全正确，这里仅提供我个人的思路和解法。

伯努利分布性质证明

思路：

伯努利分布又叫0-1分布，一个随机变量X服从参数为p的伯努利分布，其概率函数可以表示为：

化简放在本题中就是：

所以要是有求和的话就0和1两种情况加起来。

首先看第一个性质，μ是成功的概率，x取0或1，μ+(1-μ) 概率之和显然为一，

第二个要用到数学期望的公式

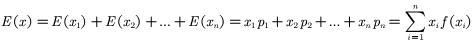
伯努利就两个值所以直接加就好

第三个要用到方差公式，这个式子显然

把刚才算好的期望代进去算就好

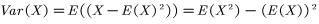
最后一个，观察式子的形式，很像神经网络在做二分类问题时经常用到的交叉熵损失函数。

交叉熵损失函数一般形式是：

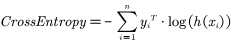
其中，y和x是m维列向量，m是y的取值数量。

当y取值为{0，1}时，就是常见的0-1分布交叉熵损失函数：

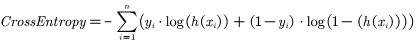
看起来很像但要证它就要了解熵的定义，简单查了一下熵的公式：

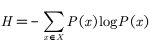
P.S. Log还是ln不重要，就是熵的单位不同而已。

在伯努利分布中就两个值，加起来就行了。

证明：